弁当のおかずの定番、タコウインナーのルーツ、寝ている時に「ビクッ」となる理由、そして算数と数学の違い、さらに数学が生活の中でいかに必要なのか…「数学は使わないから、学ぶだけ無駄!」と思っている人に、是非教えたい!
タコウインナ―が誕生した理由・寝ビクが起きるわけ・数学を勉強する意味とは?
9月19日放送のNHK「チコちゃんに叱られる!」
ゲストは荻野目洋子と溝口順平。
「なんでお弁当にタコのウインナーが入っているの?」
「なんで寝ている時に身体がビクッとなるの?」
「なんで数学を勉強するの?」
チコちゃんは、今回この3つの質問を出した…
なんでお弁当にタコのウインナーが入っているの?
〇チコちゃんの答え
お弁当にタコのウインナーが入っているのは王家の次男が少食だったから。
詳しく教えてくれるのは、NHK「今日の料理」にも講師として出演したこともある料理人尚承(しょうつぐる)さん。
実はタコウインナーを生み出したのは彼の母親。
食が細かった彼(王家の次男)のためにタコウインナーを作ってくれたらしい。
番組ではタコウインナーの誕生を「ファミリーチコトリー」※NHK「ファミリーヒストリー」形式?で紹介。
タコウインナーのルーツ
沖縄琉球王国の最後の国王、尚泰(しょう たい)が承の曾祖父。
泰の孫で承の父が明(あきら)※日本住宅公団の副総裁でダイニングキッチンを発明した人。
明は料理好きの宮城道子と結婚、2人の男の子が生まれる。
次男の承(つぐる)は食べるのが嫌で食が細く、体もガリガリの子供だった。
彼が幼稚園に通うようになり、料理好きの道子は、彼がどうしたら楽しく食べるか悩んでいた。
彼の好物は卵ときゅうりのサンドイッチ。
道子はそのおかずに赤いウインナーを入れてくれた。
当時のウインナーは皮が固くてツルツルしていた箸でもつかみにくかった。
美智子は思い切ってウインナの半分切れめを入れてみた。
焼いたら開いたので「タコみたいね」と…結果的タコの形になった。
…これがタコのウインナーの誕生…昭和34年(1959年)
全国へと広がった理由
道子の妹の朝子(料理記者)は、1968年には料理雑誌の編集長に就任する。
岸朝子と言えば、料理の鉄人の審査員で有名。
彼女が、タコウインナーは姉の道子が生み出したものだ、とメディアを通して伝えた。
朝子が幅広く活動する中で広まっていき、タコウインナーは弁当の定番となっていった。
さらに道子自身も料理コンクールで優勝したり、雑誌やテレビでアイディア料理を披露するようになった。
その後、タコウインナーは、蟹のウインナー、そして現代のキャラ弁に繋がっていった…。
なんで寝ている時に身体がビクッとなるの?

〇チコちゃんの答え…起きると寝るがせめぎ合うから
詳しく教えてくれるのは2回目の登場で以前「子供の寝相」について教えてくれた白川修一先生(日本睡眠改善協議会理事長)。
ジャーキング
寝ている時に身体がビクッとなることを「ジャーキング」といい、眠りに入る時に起きる筋肉の一時的な収縮のことをさす。赤ちゃんから大人まで枯れにでも起こる60~70%の人が経験している現象。
ジャーキングが起こる理由
起きている状態から菜無理に入る境目で起こる。
この時、脳の活動がとても不安定な状態になっている。
脳には「身体を起こす覚醒中枢」と「眠りを促す睡眠中枢」がある。
起きたり寝たりを繰り返しているのはこの中枢が交互に指定を出しているためである。
しかし眠りに入る境目では、身体を起こすか、眠らせるか、のせめぎ合いをしている。
(番組では、宍戸開とつぶやきシローが出てきて、わかりやすく説明)
通常、身体が起きている時は覚醒物質が多く分泌されている(起きろ~と信号が出ている)。
が、夜になると睡眠中枢が睡眠物質(メラトニンなど)が分泌される(静かにしなさいと指令が出て眠くなる)。
このように体内時計のリズムにあわせ覚醒交互に指令をだし起きたり寝たりを繰り返している。
睡眠不足だったり疲れている時、どうしても眠れなくて困る時にジャーキングがおこりやすい。
ジャーキングがおこる4つの原因
1睡眠不足
2激しい運動の後
3スロレスが溜まってしまった時
4カフェインの過剰摂取
例えば睡眠不足の人は本当は眠くなるはずなのに脳が興奮している…その時、せめぎあいがおこる。
この時何かの拍子で脳から間違った命令が行き、身体がビクッと動く。
この間違った司令を「脳幹網様体の異常発火」というがなんの拍子に起こるのか解明されていない。
ジャーキングは若い人に起こりやすい(理由は、日中活発に動くことから筋肉疲労も増えるから)
なんで数学を勉強するの?
〇チコちゃんの答え…論理的な思考が身につくから
詳しく教えてくれたのは、数理物理学を研究する東京大学先端科学技術研究センターの西成活裕教授。
先生は「数学を習う前に小学校で習うのは算数だが中学になると、何で数学に変わるのか?といえば、学ぶ目的が違う」という。
(※数学=一次方程式、二次方程式、因数分解三角関数√Σ…)
数学は論理的な思考を身につける
数学を学ぶ目的は論理的な思考を身につけるため。
・算数…主に日常生活でも良く使う足し算や引き算などの計算力を養うもの
・数学…問題を整理し答えを導くことで論理的な思考が身につくもの
(※論理的な思考=道すじを立てて考えること)
日常生活で数学は使わないから学ぶだけ無駄という人も多いが。数学で身に着けた論理的思考を私たちは何気ない日頃の暮らしで使っている。
一次方程式
例えば…隆君はお母さんから1000円もらった。
嬉しくてマンガ500円を買った。
お金が余ったお菓子も買いたいと思った。
一個50円だった。
お菓子は何個買えるか?
答えは10個。
これを論理的に整理して数式にしたのが、中一で習う一次方程式。
先生は「今、分かっていることは何か、分かっていないことは何か、をはっきりさせ整理する力が付く。
こういうことを無意識にできている。これ数学を学ばないとできない」という。
因数分解
因数分解も無意識のうちに日常生活でやっている。
例えばカレーを作るとする。
何も考えずにカレーを作ったら…玉ねぎを切って、鍋で炒める。そして野菜を切って炒める、その後、肉を切って炒める。まな板も毎回洗わなければいけない。
このように、カレーは玉ねぎ野菜肉をそれぞれ別々に切ると面倒くさいが、玉ねぎ、野菜、肉、それをまとめて一回で切ると無駄な作業が減る…これが因数分解。
因数分解を学ぶことで同じような作業をまとめる力がつき、効率よく仕事ができるようになる。
数学をさぼっていたら…
6年間(中学・高校)かけて習う数学、方程式や因数分解、微分・積分など、言葉以上に内容を思い出せない公式…
先生によれば「数学をさぼり論理的な思考が出来なかったら、聞いている方がわからないぐらいぐちゃぐちゃな話をする大人になる。自分の言っていることが相手に伝わらないということが起きてしまう」らしい。
サイン コサイン タンジェント
直角三角形の(辺の)比率を表わしたもの、これが私たちの生活にも役立っている。
直角三角形の直角を右下に置いた場合…
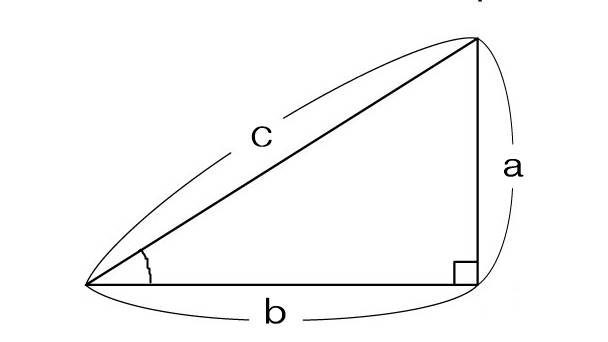
aとcの比率:サイン【sinθ=a/c
bとcの比率:コサイン【cosθ=b/c】
aとbの比率:タンジェント【tanθ=a/b】
…とそれぞれの名前を付けたもの。
これを使う事で、人の身長を直接測らなくても調べることができる。
そこで、先生は床に三画定規を置き、スタッフの頭の位置と定規の先が重なる位置を見つける。
先生が持っている定規の高さは7㎝、長さは12㎝、スタッフとの距離は2m88㎝だった。
スタッフの身長求める場合、タンジェントの数式【tanθ=a/b】にわかる数字を当てはめればいい。
a=7
b=12
なので
tanθ=7/12
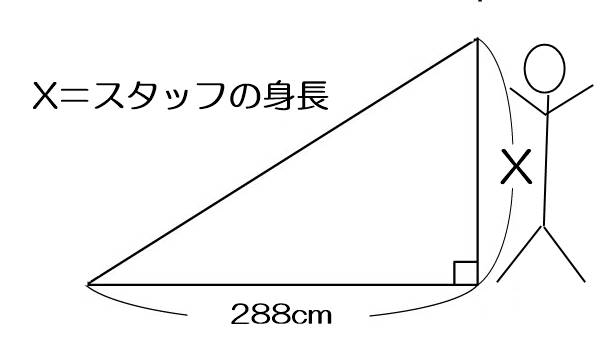
スタッフまでの距離が288㎝だったので
x=288×7/12
x=168
…168㎝と答えが出た。
正解だった。
例えば、富士山や東京タワーの高さを知りたい時、この三角比(サインコサインタンジェント)を使うと地面の長さで高さを調べられる。
富士山の高さの求め方
1、山頂と直角三角形の定規の先が重なる場所を見つける。
2、そこから富士山までの直線距離を地図上で測る。
3、測った距離に直角三角形の比率を当てはめて計算する。
…富士山の距離が出る。
まとめ
私の知人の話。
彼の職場に70才ぐらいの同僚がいるという。
知人によれば、その同僚との会話にはいつも苦労しているという。
何を話しているのかわからないというのだ。
例えば、今勤めている会社の話をしていたはずなのに、なぜかだんだん話が食い違ってきた(こっちが知らない人の名前が出てきた)。よくよく聞くと同僚は前に勤めていた会社の話をしていた…なんてことがあったらしい。(これは一次方程式がわからない?)
年齢のせいだろう、と思っていたが今回の数学の話を聞いて、実はこっちのほう(数学が苦手)なのではないか?と思うようになったという。
さらに、例えば、6ヵ所の建物の掲示板に掲示物を1枚ずつ貼るという仕事があるとする。普通の人は、テープと掲示物をもってその場で貼っていく。この方法が早いし合理的だろう。が、その同僚は、いちいちテープが置いてある管理棟に戻って2枚の掲示物の用紙4ヵ所にテープを貼って、両手に持って歩くらしい。
これはもしかしたら因数分解が解けない?というパターンではないだろうか?
…と知人と話したが、あながち冗談ではないかもしれない。

